March 22, 2020 – When I was in college I took geology classes, enough for a Bachelor of Arts in Geology; although my ultimate degree, on the paper, was a business degree in finance because my University wouldn’t let you have a degree from two colleges within the university. Geology is a college. Business is a college, both within the University. I had to pick, and finance was employable, geology was not. The crazy thing though is that the College of Geosciences has me on their list to this date as a graduate; I get a really cute Christmas card from them every year. I get their newsletter too. The College of Business sends me occasional things asking for money. So over time, despite what the diploma says, I have come to consider myself a geology graduate. Remember though, I have the requirements for a BA, not a Bachelor of Science, and that’s important, because I have a complex about it.
In my day, the acronym they have now for all things science didn’t exist; STEM, they call it now: science, technology, engineering and mathematics. Also, in my day, there were almost no females in anything science. Biology, yes; geology, there were a handful of us. Honestly though, there weren’t many of anything in geology when I was in college. After all, it was in the ‘80s, after the oil business had tanked, and geologists are usually trained for the oil business. But back to that BA vs. BS degree thing, if I had taken all of the math I needed for the BS, then I couldn’t have used my electives to get the more employable finance degree, and there really weren’t females in those classes (being pre-STEM of today), so I opted to complete the requirements for the BA, but then get the paper from the business college. Why is any of this relevant? Well, because for decades I thought I cheated myself out of the math. I thought I couldn’t do it. Fast forward a lot of years.
Sometime after 9-11, I became completely fascinated with a physicist named Richard Feynman. I was completely taken by how things work from a physics standpoint. Feynman wrote books, two that are meant as anecdotal stories of his life that tell things about physics, and his own greatness – he co-holds the Nobel prize for inventing quantum physics (the physics of particles) and was the person who determined that the O-ring failure brought down the space shuttle Challenger. I read those more simple books. Then I read a short book Feyman penned with individual chapters about physics, the major topics. I read that book on a plane. There was a guy sitting next to me wanting to know what I was reading. He probably thought, there’s a crazy person next to me reading physics for fun. But, for me, it was fun. It was fun because it was a challenge. The trouble was, I wanted, really badly, to actually understand it. And that requires a real understanding of math.
Math. If you say the word to someone who has actually studied it, “math” starts when you first see what they call a function. Before that, it’s not math. It’s arithmetic. A lot of math problems turn into arithmetic as they are solved, so arithmetic is important, but it’s not math. Math starts at calculus.
In college, I took Calculus I, and I took Calculus II. They were nightmare classes, hundreds of people in a room, with some person with an incomprehensible Asian accent talking making your white-ass feel so much lesser if you couldn’t see it. What I mean by see it is explained only by my own experience with Algebra.
Algebra is the basis of it all. It’s not math, but it’s important. It’s how you get a tangible answer you can understand. And contrary to the opinion most people hold when they are taking it in high school — that you’ll ever use it — I use it all the time. It’s how one calculates a rate of return in real estate. It’s important in determining certain tax formulas. I can now, and always have been able to, feel it, to understand it to its root, implicitly. In college though, when I got to Calculus (the mistake being not taking Calculus in high school), I couldn’t feel it. It seemed to be only memorization. It was frustrating. I went from someone who in high school could get into theoretical discussions with the math teachers; people would ask me to do it just to slow down our progress when we all didn’t want homework over the weekend. I just looked like a dumb baton twirler; okay I was a dumb baton twirler who was good at algebra. So my frustration in college at not innately feeling calculus stopped me in my tracks. No Bachelors of Science because, in geology, that took more math than Calculus II. And I would have to actually understand it to take more math after Calculus II. You see, math is like skating where the lowly three-turn morphs into every jump you’ll ever do; in math, you must master the first concepts to learn the next ones. No way. That was my thought then, no way could I do it. I’d have to settle with the “arts” part of the degree, not the “science” part of the degree.
But…These decades later, I wanted to understand what Feynman was talking about. And I wanted to prove to myself I could have done it. So, I enrolled in the certificate program at UCLA for math.
I did math every day. The classes were at night. I did homework around that. And I had my law practice. I had skating too. I pretty much never did much else. And I did it for no reason other than to learn. Actually I take that back because my brain became sort of a human-calculator. I got really got at doing arithmetic. It’s like a good party trick, or something. Let’s watch Whisper do fractions in her head.
I took all of the math I couldn’t do before. Until I got skin cancer, and even then, the teacher said he’d promote me going into the school to get an actual degree because my love for it was that apparent. I missed a test, because of that surgery I had in 2005, and bandages covering my nose and all, he sat me in his office so I could take the last test. The trouble was, the next classes were every day in the middle of the day, so I didn’t finish. That was the end of my math career. Well, except for the human calculator skills I still retain.
Don’t get me wrong, I’m not smart. I didn’t retain as much real math as I would have liked, not the level that would let me read any real physics, but I do have the party-trick calculation skills, and I have enough math skills to know when I smell a rat.
And here it is. All of this stuff about Coronavirus, from what they are doing, to the answers to the questions in my last article — the when will it end, what’s going to happen — all come down to math. They, our leaders, are looking at math curves to decide our fate, as scary as that is.
Mind you, I doubt any of them can do even rudimentary algebra. They are probably like my clients who, despite having tens if not hundreds of times my net worth, which automatically makes them smarter than I am, just ask them, always ask me, what do you divide by what to get to the rate of return they are making. Every time. You think they’d write it down by now. But the math that’s controlling our lives right now is not algebra, as rates of return calculations are, except in one sense which I’ll get to; it’s Calculus. In fact, it’s Calculus II. But let’s start with the algebra. And don’t be scared. It’s actually really easy.
Let’s call this Course 1: Algebra for Corona.
They say, from the experience in China, that 80% of the people who get coronavirus have only mild symptoms. I’m going to assume for these purposes that all the population has been tested to come to that 80% number, but honestly, from everything I’ve read, I really don’t know if that’s true or how they got the 80% number. The remaining 20% get sick, many with horrible pneumonia that requires ventilators. That’s no joke either.
We know here in the U.S., they aren’t testing, generally. And when they test, the test they use is a swab test, like when you have strep throat. That’s a test to look for active virus on your throat. But, the U.S. CDC is not allowing the use of that test for anyone unless the patient is symptomatic. And to get the test, the patient needs to be in a place that will allow the test, like the hospital. Mind you, I haven’t seen a hospital lately, and I’m not going to go, hopefully, but from what I’ve read, the people they are testing are the ones who are sick. How sick, they aren’t saying, but sick. I think that means the ones who are needing hospital care. In other words, those seem to be the 20%. And here’s the algebra on that.
If the models here are like they are in China, and those sick people we have here are the 20% (because the 80% have mild symptoms and aren’t getting tested), then the algebraic formula for how many people actually have coronavirus is explained as follows:
The number tested who are sick/20% (that slash is divided by). At the current count of cases in the U.S., namely 26,909 cases as of March 22, 2020, that means the real number of cases, including cases that are not tested, is 134,545 cases (26,909/.20, which in words is 26,909 sick people divided by 20%). The numbers for the world as of today is 321,000 tested sick/.20 or 1,605,000 total sick, which includes everyone, the asymptomatic, mild cases and those 321,000 sick people.
Reversing it, just to check, that means in the US, we have, out of 134,545 cases, multiplying by 20% (.20) 26,909 cases of sick people, and 80% (.80) or 107,636 people who aren’t so sick, but are out there. Fun.
They say there are more people walking around who are sick and don’t know it, but say they don’t know how many. It’s not that hard. There are 107,636 of those people.
The next course is a bit more advanced than algebra. It’s our first function, meaning real math, but it’s not that hard either. Here we go.
Let’s call this: Course 2, Pre-calculus for Corona
In regular pre-calculus, we learn about functions, meaning the change in some number with respect to another. Not that hard, really. There are a lot of graphs. Think of a simple one. You put a dollar in your drawer every day. And you make a graph of it. On the graph, the dollars are on one margin, time is on the other. Usually “time” is on the bottom horizontal line and the other thing, here money, is on left vertical line. If you put one dollar in every day, the line will go up at an angle to the right, at a steady climb. Easy. In fact, that’s an algebraic line formula for it (Y = MX +B), but I won’t get into that.
Hard graphs are when something goes up faster. Really smart mathematicians who lived long ago devised formulas to draw these lines. And they aren’t lines. They’re curves. The one we hear of now is called an exponential curve. A true exponential curve starts small, curves up, then becomes a straight line up with no end in sight.
Viruses grow exponentially up at a rate that can be measured from cases, new cases compared to old. But at some point, either people die from the virus and the line can’t grow any more, or people recover and the line starts to fall. Plus the line starts to fall from what they call herd immunity. That means once someone recovers, they can’t get it again, and then the virus dies off because the virus can’t find a new host. In that instance, when we have herd immunity, the exponential curve falls at about the same level to the right, turning our graph into what they call a sine curve or a parabola.
Herd immunity is mathematically related to the transmission rate. They are reporting that in the U.S., the transmission rate of coronavirus is 2 to 2.5. Not that I fully understand this math, without really getting my books out and studying, which I might do, but from the graph, herd immunity seems to require half of the people in the population to develop an immunity to coronavirus for the sine curve to go down at the same rate on the right side as the increase on the left side.
The rate of climb of the graph depends on various factors in the equation. That’s what they are manipulating, with math experts and their computer simulations altering the numbers. If they lock us up, that affects the transmission rate, which will affect the slope of the line. In other words, they are trying to change the 2.0 to 2.5 number, so the graph doesn’t climb as fast.
Or, theoretically, if you could isolate all of the cases, with broad testing, and then let the virus die off in those people, without having much, if any additional transfer rate.
Or … a combination.
My question is what is the rate of transmission they are after (theoretically less than 1, but they’re nowhere near)? What is the time they are after? Where is the graph that shows time on the X-axis? In other words, how long do we have to be locked up in this nightmare economy? And what exactly are they doing? The graphs will show. They will show the plan.
One would think you could find these graphs, that the graphs would be readily available, but they are not. And they certainly don’t show the time part of the X-axis. I mean, really, do they think people can read these graphs? Do they think any of us paid attention in higher math class? Why not put them out there?
Just so you know, I spent hours looking for graphs. And the most common graph I’ve run into is the flatten the curve graph. Mind you, we’re now going into the third class. So a little prefacing knowledge is useful.
Class 4: Calculus II for Corona:
I’m saying Class 4 because these graphs require knowledge of integrals. Area under the curve calculated based on a sine curve is Calculus II — integrals.
Overall, what calculus is used for is to measure things that are not straight; in other words to measure things that are round, or roundish. It was invented to measure orbits of planets and things like that. It’s a summation approximation of the size of the area under a curve, done by taking integrals of crazy things. Yeah, whatever. What it does is measure the amount of stuff under a curve.
Remember, a virus makes a curve, a sine curve, meaning it goes up, then forms a round-like shape at the top where it levels off, then it goes down the other side at about the same rate as it came up once people have natural immunity. The area under that curve is the number of real-life human beings who will get sick. We are the stuff under that curve.
The mantra now is flatten the curve. What I had hoped, is that they wanted to turn an otherwise exponential curve, meaning one that’s charging up at a really fast rate, into one that all of a sudden stops and goes down. Flatten, meaning make it linear, like my dollar in your drawer example. But that’s not what they are saying.
What they mean is to stretch out the sine curve. It looks like a mole-hill when it’s stretched out, instead of a mountain, which it looks like if it’s not stretched out. But from a Calculus II standpoint, the area under the curve — meaning the numbers of us who will get sick — is the same in either curve. They just are stretching out our sicknesses over a longer period of time. It’s that magical X-axis of time. More time. Think of this in terms of a pile of dirt. You can pile the dirt really high, or you can smush it down. This flattened curve they want is just a smushed down round thing, a smushed down sine curve. But it’s the same dirt in the piles, and it’s the same number of people in both the tall sine curve or the smushed longer-in-time sine curve.
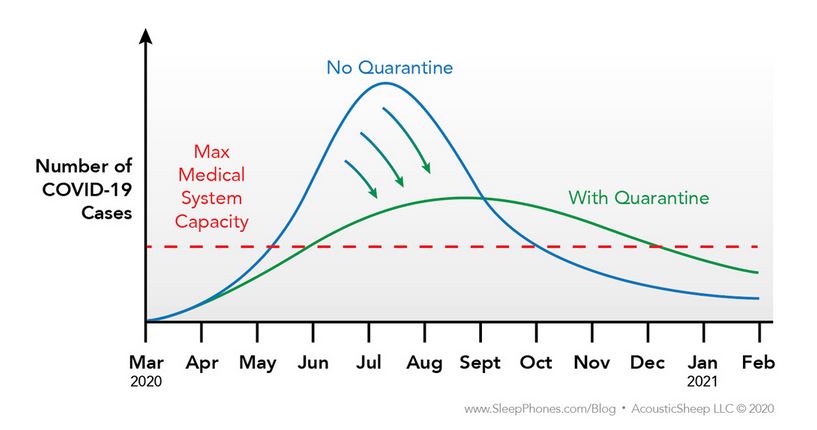
I think this graphic shows it well. The blob just moves. The same number of people get sick.
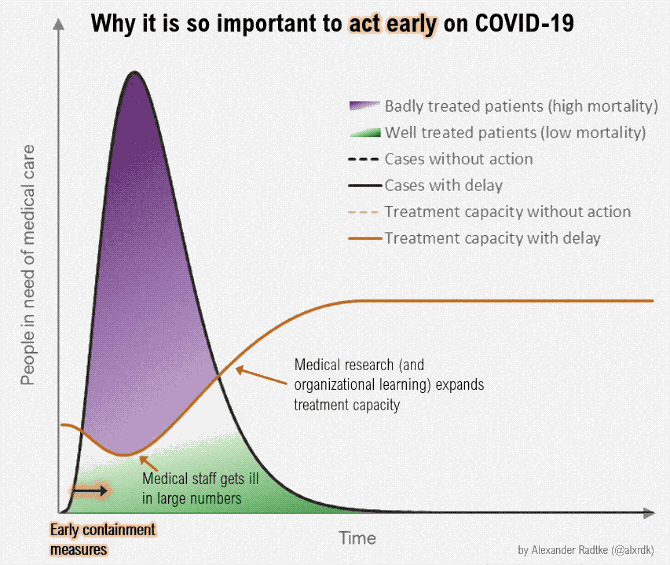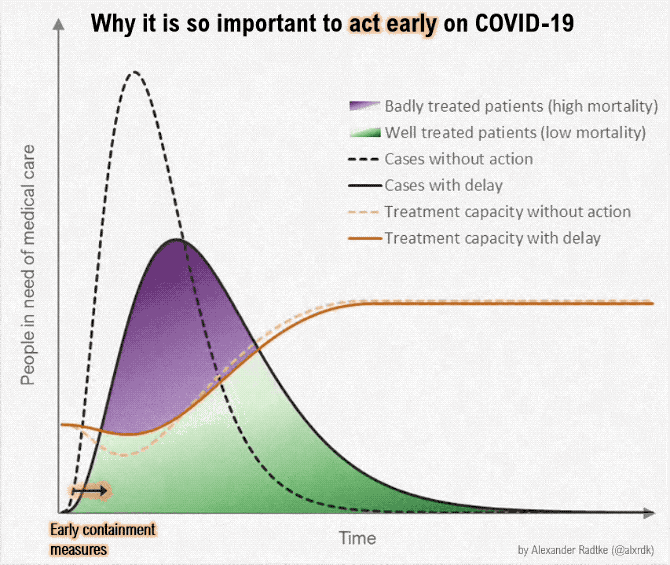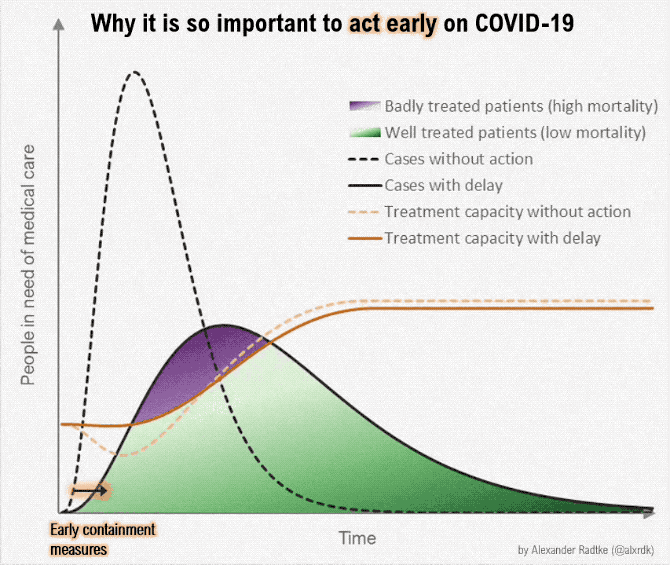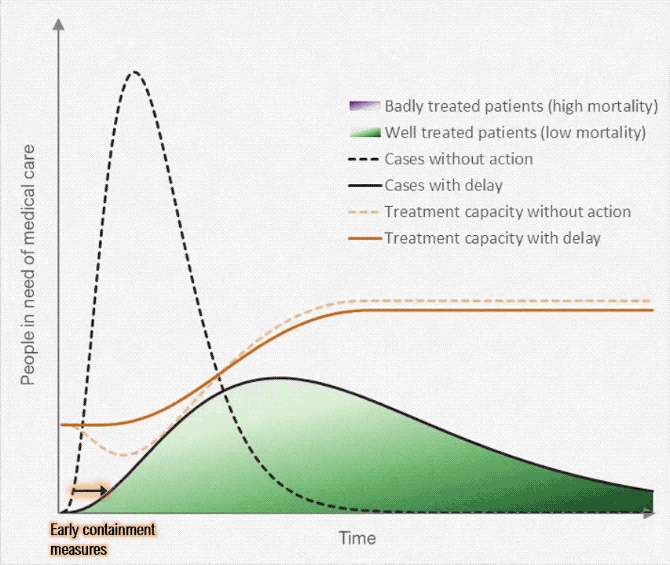
Mind you, the goal of this flatten the curve thing is to not overwhelm the hospitals, doctors, nurses, physician’s assistants and technicians, to keep the number of sick at any one time at the point where the sick can get a hospital bed. And that’s great. Hopefully those people save the most sick of us, the 20% that we are testing now. I am thankful for those people, the doctors, nurses, physician’s assistants, and hospital workers, all working tirelessly to save the people they can.
The flattening is also to give us time to get a vaccine, or so they say. But if they stretch this curve so that it lasts the 18-months it takes to develop a vaccine, assuming they can make one in 18 months, then will any of us be employed by then? Maybe some of you. And if they think their proposed $1,200 will matter for anyone who truly loses their job or their small business, think again.
But let’s talk about what’s missing from these graphs. And that’s the markings. They don’t have numbers, no numbers on either the X-axis (the horizontal line for time, to say how long this is going to take) or the Y-axis (the vertical line for how many of us are going to get sick, really sick). And I’m actually not sure if these flatten-the-curve graphs count only the 20% sick out of the entire 100%, because now there is talk that there will not ever be any widespread testing. And actually, I think the graphs count the 20% who get really sick, but even so, the 20% are a part (a sub-set) of the greater number, the herd, so the total graph will have the same shape. Plus, that means they have to be taking the 20% from their count of herd immunity over time, and I’ll get to that.
I spent a long time trying to find graphs that showed the marks on the X-axis for time. I found two. One showed the flattened curve finally tapering out in February 2021. The other was within an article written by Senator Marco Rubio (Republican of Florida). They are below.
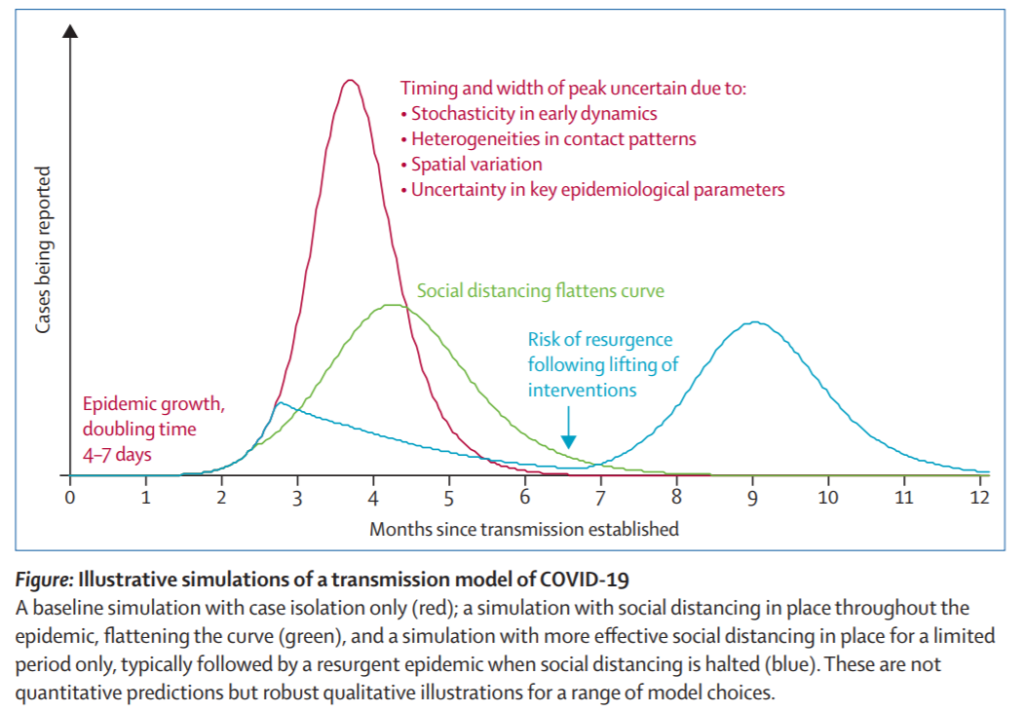
First of all, could this (first graph) be the graph the senators are using, since a senator put it in the article? If so, who made the model? And on what assumptions? And let me tell you, if this is the graph they saw in January when some of them sold their stock, that’s really bad. Oh and they did nothing then to help us, no pre-ordering of tests, no warnings, no nothing. I’m beginning to believe this is the real graph, and that they had it in January. Sad. But back to the graph.
The red line looks pretty accurate compared to the daily totals. I think we are at about “month 2.5”, but who knows (also really scary if month one was when they sold their stock). Okay, so red is obviously really bad. It doesn’t show where the health care capacity is on this one, but presumably around the lower peaks of the green and the blue line. The green line is to represent efforts to flatten the curve meaning stretch the number of people getting the disease from months 2 through 5-ish to months 2 through 7-ish (which means we have five months of this). Then there’s the very curious blue line.
The beginning of the blue line shows what I had hoped they were doing with all of these closures to flatten the curve, meaning lock everything down so the disease makes the number of overall sick people lower, and then the line would go vertically down (the best case ever and what I wish were true). The beginning of the blue line is going up exponentially, then at the place where I think we are (month 2.5), everything comes to a screeching halt, people go inside, and the virus stops infecting new people, with the already-sick recovering and the virus finding no new hosts. Notice, even in that scenario, we still have to get through 4 to 4.5 more months (two to three more months) before all of this sequestering stops.
And the really scary part is if they let us out, when they let us out, they think the blue line just becomes the green line, only later. The reality of the blue line I think is that they are locking us up to think they are doing something, knowing all that can be done is herd immunity, which they’ll put us through later.
Herd Immunity
A have read a lot of articles from the U.K. Their government’s statements from the beginning were that they want to fight coronavirus with herd immunity. People there wanted the lock downs, so some of the lock downs are happening now, but they are about the same, if not slower than we are, about testing. Seriously, first world countries, and we aren’t doing wide-spread testing.
The flattened curves sound good. We can think they are keeping us safe, that we aren’t going to get it. But we are, we are going to get it. I’m not a fan of California’s governor, but at least he told the truth: 56% of Californians are going to get this. The reality is that same percentage of everyone, everywhere, is going to get this. From looking at the graphs, and looking at the transmission rate of 2 to 2.5 people infected for every sick person, that’s the percentage that creates herd immunity – 50-56% of all people have to get a disease with a 2-2.5 people transmission rate to stop the virus with natural immunity. They are only controlling the X-axis – time—spreading out the time in which we develop herd immunity so that our health care system can take care of the sickest among us.
We will never test. Not until they come up with a test that tests whether you’re carrying immunities for it. And it doesn’t look like there will be a vaccine.
Is it the end of times? Probably not. Statistically, yes more math, if you’re not over 65 or have a compromised immune system, you’re probably not even going to notice getting sick. You might have already gotten it. Maybe you’ll be one of the 100% minus 56% who doesn’t get it, but then you won’t be immune, so eventually you will get it. But this chart disturbs me. This chart is the chart showing the percentage chance you’ll die if you get it, mind you die of a gnarly, horrible thing. Statistically, the numbers are such small percentages for any age group less than 50 years of age, that you might as well not count that. But remember that 20% sick number? Look at the breakdown here: 4.5% if you’re over 60; 9.8% if you’re over 70, and 18% if you’re over 80 years old; if you’re in those ages, that’s your percentage chance of getting really sick and then dying.
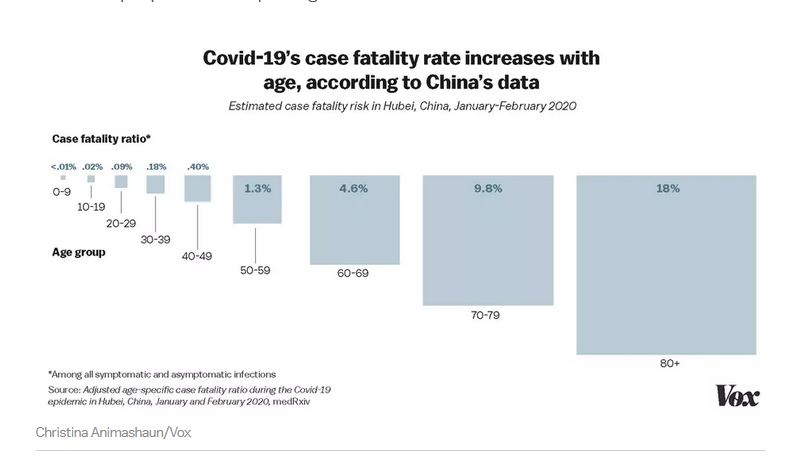
This is herd immunity at the expense of vulnerable people. And it’s sad. And come one year from now, I’m certain every one of us with know someone who died of the coronavirus pandemic despite all efforts to spread out the curve to help the health care system handle the sick.
But getting back to that blue line, when they let us out, why will it not simply become the red line? If there are no controls on us, what’s there to keep the transmission rate from returning to 2 to 2.5, which is the red line? There is no explanation for that. Not at all. Also, that blue line? That’s an imaginary line because the cases are still going up, matching the red line, no matter what we do. New cases are not dropping down in vertical line, as depicted on Marcio Rubio’s blue line. Perhaps in the next few weeks, the curves will start to look like the green line; I have no idea, but that’s all we are ever going to do. That blue line would happen only if we could or would test the general population instead of waiting for the very sick to go the ER to get the few tests they are giving out. And we don’t, and aren’t, going to test.
The bottom line: we are a herd. We are the area under a sine curve of a calculus problem that I’m pretty sure nobody in Congress understands, if they ever took Calculus II in the first place. I’m not sure if we will get to the flattened curve of the green line, or how long they’ll keep us there. I’m not sure if the five- months-from-now estimate of Marco Rubio’s chart is it, or if the February 2021 chart (above) is it. But any way this goes, I think California governor’s statement that 56% of the people will get it is true because all they are capable of doing is letting herd immunity take its course, and 56% of people must get it for herd immunity to happen.
Let’s hope we all get immune faster than they say. Power to the people! Here’s something happy. Ford, taking action. Let’s hope we all do. That’s what I’m doing.
